Normal Dağılım

Normal dağılım aslında öğrencilik yıllarında bir çok kişinin “çan eğrisi” olarak duyduğu dağılımdır. Normal dağılım eğrisinin şekli bir çana benzediğinden çan eğrisi olarak adlandırılır. Gauss dağılımı olarak da bilinmektedir.

Normal dağılım, simetrik dağılımın bir türüdür. Simetrik dağılımlar, bir bölme çizgisi iki ayna görüntüsü oluşturduğunda ortaya çıkar. Tüm simetrik dağılımlar normal değildir, çünkü bazı veriler normal dağılımı gösteren çan eğrisine ek olarak iki tümsek veya bir dizi tepe şeklinde görünebilir.

Normal dağılım modeli, değişkenlerin örneklendiği dağılım türüne bakılmaksızın, bağımsız, aynı dağılıma sahip rastgele değişkenlerden hesaplanan ortalamaların yaklaşık olarak normal dağılıma sahip olduğunu belirten Merkezi Limit Teoreminin (CLT) anahtarıdır.

Neden Normal Dağılım?

Normal dağılım 19. yüzyılda birçok doğa olayının ortalamadan “normal olarak saptığını” gösteren bilimsel yayınları takiben “normal” terminolojisini almıştır. Bu “normal değişkenlik” fikri, doğa bilimci Sir Francis Galton tarafından 1889 tarihli Natural Inheritance adlı eserinde “normal eğri” olarak popüler hale getirilmiştir. Ayrıca normal dağılım;

• Doğal Olaylarda Sık Görülür: Boy uzunluğu, ağırlık, IQ gibi birçok insan özelliği normal dağılıma yakındır.
• İstatistiksel Çıkarımlarda Kullanılır: Örneğin, bir ürünün kalitesini değerlendirmek için örneklem alınır ve bu örneklemdeki verilerin normal dağılıma uygunluğu test edilir.
• Olasılık Hesaplamalarında Kullanılır: Normal dağılım tabloları kullanarak, belirli bir aralıkta bir değerin bulunma olasılığı hesaplanabilir.

Ortalama ve Standart Sapma

Standart normal dağılımın iki parametresi vardır: ortalama ve standart sapma. Normal bir dağılımda ortalama (ortalama), medyan (orta nokta) ve mod (en sık gözlem) eşittir. Bu değerler tepe veya en yüksek noktayı temsil eder. Daha sonra dağılım, genişliği standart sapma ile tanımlanan ortalama etrafında simetrik olarak düşer.

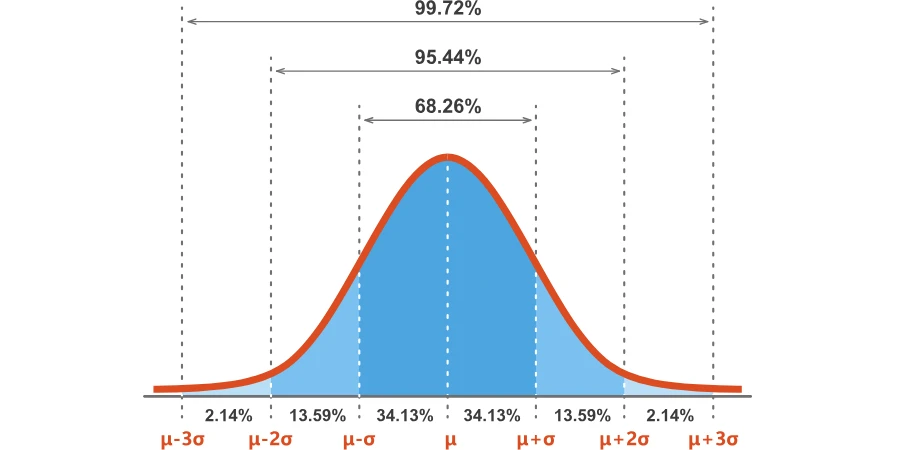
Ampirik Kural

Tüm normal dağılımlar için gözlemlerin;

• %68,2’si ortalamanın artı veya eksi bir standart sapması içinde;
• %95,4’ü +/- iki standart sapma içinde;
• %99,7’si ise +/- üç standart sapma içinde;
• %99.98’i ise +/- dört standart sapma içinde yer alacaktır.

 

Neden Önemli?

Veri analizinin ilk adımı normal dağılıma uyumluluğu test etmektir. Yani elinizdeki veri seti için yapmanız gereken ilk analiz bu verilerin dağılım tipinin normal olup olmadığını bulmaktır. Eğer verileriniz normal dağılıma uygun değilse bu durumda başka bir dağılım ile veri analizine devam edersiniz.

Normal dağılım eğrisi hep aynı mıdır?

Normal dağılım eğrisi her zaman simetrik olmayabilir, sağa ya da sola çarpık şekilde normal dağılım eğrisi de görebilirsiniz.

Normal Dağılımın Özellikleri

• Çan Eğrisi: Grafikte çan şeklinde göründüğü için çan eğrisi olarak da adlandırılır.
• Simetri: Dağılım, ortalama (ortalama değer) etrafında simetriktir. Yani ortalamanın solundaki değerler, sağındaki değerlere benzer bir şekilde dağılır.
• Ortalama, Medyan ve Modun Eşitliği: Normal dağılımlarda ortalama, medyan ve mod aynı değere eşittir.
• Standart Sapma: Verilerin ortalamadan ne kadar uzaklaştığını gösteren bir ölçüdür. Standart sapma büyüdükçe, dağılım daha geniş yayılır.

Normal Dağılımın Kullanım Alanları

• İstatistik: Verilerin analizinde, hipotez testlerinde ve güven aralıklarının belirlenmesinde kullanılır.
• Kalite kontrol: Üretim süreçlerindeki varyasyonları analiz etmek için kullanılır.
• Finans: Hisse senedi fiyatları, getiriler gibi finansal verilerin analizinde kullanılır.
• Sosyal bilimler: Anket sonuçlarının analizinde, psikolojik testlerde kullanılır.
• Doğal bilimler: Fiziksel ölçümlerin analizinde kullanılır.

Standart Sapma

Standart sapma genel olarak niceliksel ölçekli sayılar için en çok kullanılan verilerin ortalamaya göre yayılmasını gösteren bir istatistiksel ölçüdür. Eğer birçok veri ortalamaya yakın ise, standart sapma değeri küçüktür; eğer birçok veri ortalamadan uzakta yayılmışlarsa standart sapma değeri büyük olur. Eğer bütün veri değerleri tıpatıp ayni ise standart sapma değeri sıfırdır.

 

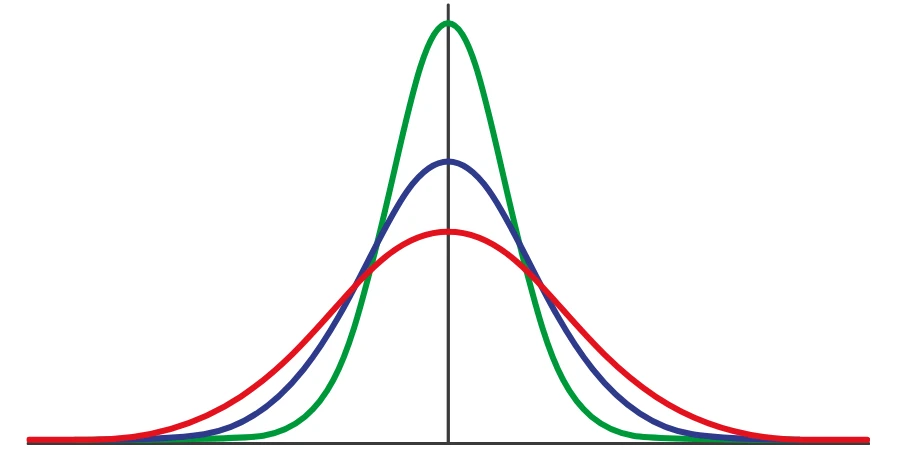
Normal dağılımın iki önemli parametresinden biri olan standart sapma günlük hayatta bize ortalamadan çok daha fazla bilgi verir. Özellikle süreçlerinizdeki verileri incelerken sadece ortalamaya bakarak değil standart sapmayı da işin içine dahil ederek karar vermeniz gerekir. Çünkü yukarıdaki şekilde de görebileceğiniz gibi, ortalamaları aynı olsa bile 3 normal dağılım eğrisinin standart sapmaları birbirinden farklı. 

Düşük bir toleransla ürün üretmeniz gereken bir süreciniz varsa daha kararlı bir prosese ihtiyaç duyarsınız, bu nedenle standart yeşil renkli eğride olduğu gibi düşük olmalıdır.

Günlük hayatta karşınıza çıkan yaş, kilo, boy vb. gibi araştırmaların çoğunda normal dağılım üzerinden yapılmış analizleri görmeniz mümkündür.

Konuyla ilgili bir başka yazıma buradan ulaşabilirsiniz.

Konuyla ilgili dış kaynak için buraya göz atabilirsiniz.

Sevgilerimle,

Lean Teacher